Maths Mastery & KS2 SATs - Moving From Formal to Flexible
Estimated Reading Time - 7 minutes
Introduction
KS2 SATs might be over for this year, but what can we learn from the tests to help us better prepare future Year Six cohorts for this assessment of maths mastery?
With opportunities to use and apply their maths facts, and questions that could be solved using formal methods (such as column addition and subtraction, long multiplication and division), there were plenty of chances for the savvy student who is a flexible thinker to save themselves some time and reduce the workload. But, how many pupils were well-prepared for these moments and how many took the opportunity?

This blog will look back at some similar examples from previous year’s KS2 SATs papers. The 2022 KS2 Maths SATs papers will be reviewed at our autumn Maths Subject Leader Briefing – further details can be found at the end of the blog.
Know your times tables facts!
We know the Government are keen for every pupil to be fluent in the multiplication (and division) facts for the times tables up to x12, afterall, that’s the reason we now have the Multiplication Tables Check to contend with each summer. However, it’s not just knowing their multiplication facts that’s important, it’s seeing the opportunities to use and apply them!
Take a moment to look through the arithmetic and reasoning papers from any year post-2016.
How many questions rely on pupils having their multiplication facts at their fingertips?
But they can work them out in the test!
Well, yes…they can, but how much more efficient are they if they have those facts stored in their long-term memory? Freeing up pupils’ working memory is crucial for them to be able to cope with the demands of the test. Counting out their six times table on their fingers to work out the perimeter of a hexagon is not only time consuming, it can be distracting and lead to inaccuracies in comprehending the question or following a complex method or procedure through to the end. Take this question from Reasoning Paper 2 (2019):
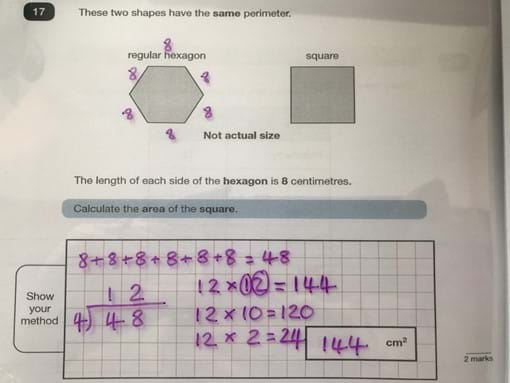
Just knowing that 6 x 8 = 48 and that dividing 48 by 4 is 12 frees you up to work out the trickier multiplication 12 x 12 (if you didn’t already know it). In 2019, most pupils used formal methods to calculate each of these facts which is inefficient and tiring.
Which multiplication facts to they need to be proficient in?
All of them of course!
Having said that, some are more likely to be integrated into the SATs questions than others; although some of the easier times tables are incredibly helpful as a route to knowing harder facts. For example, a child who has not yet secured their eight times table can make very effective use of doubling, if taught this as a strategy, to get around their lack of the full range of tables facts. Flexible ways of working are key!
Just as in the Multiplication Tables Check, some times tables will appear more frequently; the same is true in the SATs it seems. Of course, it’s not the easier ones that appear more often either, meaning those pupils who have a secure knowledge of the facts beyond the twos, fives and tens will be at a distinct advantage.
Formal methods have their place - but how does flexible thinking help?
We’ve all watched in agony as a pupil works through a complicated formal method to solve a calculation that just doesn’t warrant the time and effort that the child is investing. In fact, many adults are heavily reliant on formal methods because that is the way they were taught. However, is being procedurally fluent the key to being a proficient mathematician?
Take this example from KS2 Reasoning Paper 2 (2018):
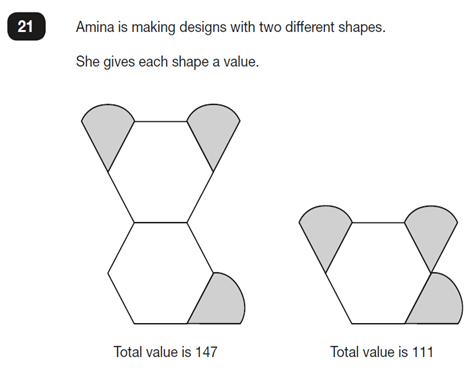
Seizing upon the numbers lead some pupils immediately towards their procedural knowledge.
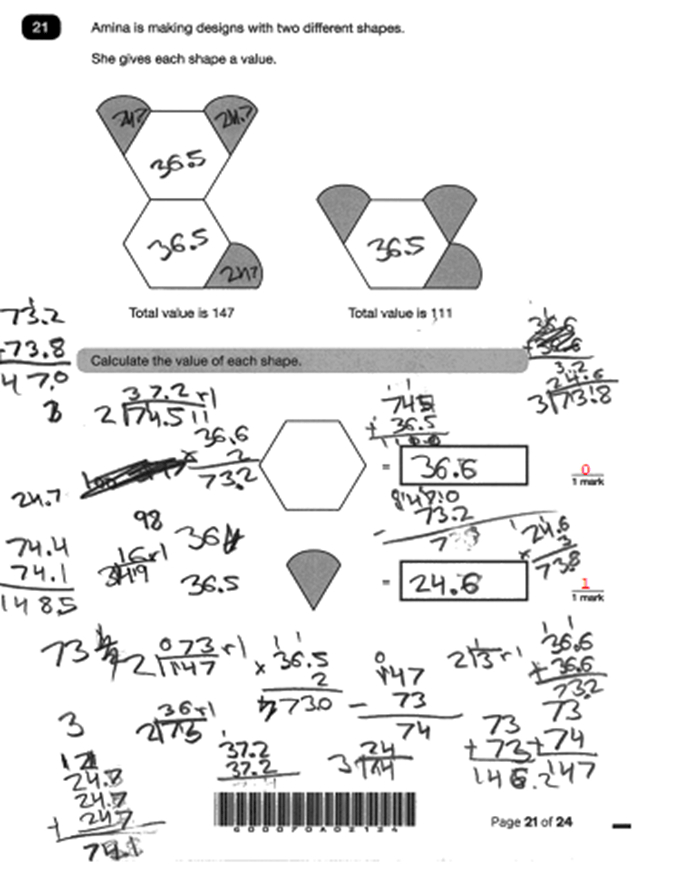
Taking time to stand back and look at the bigger picture, you realise that the difference between the two designs is just an extra hexagon in the left-hand diagram. Simply subtracting the 111 from the 147 gives you the value of one hexagon. This is a calculation that most Year 6 pupils should be able to attempt mentally or with some informal jottings such as a number line.
Having worked out that the value of one hexagon is 36, they can subtract the hexagon from the right-hand shape (111 – 36) to find that the value of the 3 ‘fan shapes’ is 75. Making the connection to fractions and decimals helps here because pupils should know that there are three lots of 25 in 75. Again, using and applying not just our number fact knowledge but showing flexibility by connecting different areas of mathematics.
Step back and ask - What do you notice?
The question ‘What do you notice?’ is such a simple, yet powerful question but one that is often missing from the classroom, particularly in maths. We are all guilty of being too quick to look for the ‘answer’, but surely the journey is as important, or even MORE important?
Take a look at the subtraction 582,346 – 198,000. At first glance, many children (and adults) will assume the need for a formal method, or a complicated method of rounding and compensating (198,000 is close to 200,000 so I’ll round it up and take away 200,000, then I’ll add 2,000 back on).
But is there a simpler way?
How about using non-standard partitioning? This is a technique which involves partitioning a number into useful parts.
How is it different to standard partitioning? Well, standard partitioning involves breaking a number into its place value parts (or its column values), so 582,346 would break into 500,000 + 80,000 + 2,000 + 300 + 40 + 6. In the case of this calculation, standard partitioning is not very helpful, yet it is the default mechanism for most of us, children and adults alike.
Here, non-standard partitioning is much more helpful, but may not be a way you are familiar with working or yet feel comfortable using. Let’s see how it makes this calculation easy to tackle mentally.

On the right, you can see that we’ve partitioned the 582,346 into 200,000 and 382,346. Now, we can leave the 382,346 untouched and concentrate on the 200,000. From this we can subtract the 198,000 (by Year 6, we can probably manage this mentally, without even using jottings). This of course leaves us with 2,000. So now, in one side of our bar model we have the untouched 382,346 and on the other we have the remaining 2,000. Again, we probably don’t need a formal method, or even jottings, to add these two numbers together.
The advantage of this method over the rounding and compensating method is that we don’t find ourselves with a group of very confused pupils who are not sure what to do with the 2,000 they have to deal with after rounding up the 198,000.
One last gem of a question...
To top off a challenging reasoning paper, in 2016 (Paper 3) pupils were faced with this final question:

Most pupils were unable to tackle the question because they didn’t have a secure understanding of the relationship between multiplication and division. Because they weren’t able to visualise what the question was asking, it was also difficult for them to explain their reasoning.
However, look how simple it becomes when we adopt a more flexible approach and stop thinking about long multiplication or bus stop methods!
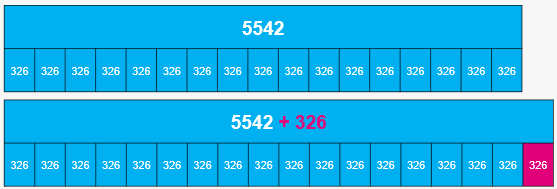
This bar model beautifully exemplifies the structure of the mathematics in this question. What’s more, it also enables pupils to articulate a clear response: 5542 ÷ 17 = 326 is the same as 17 x 326 = 5542, in other words, 5542 is 17 lots of 326. So, to find out 18 x 326 (or 18 lots of 326) we just need to add another lot of 326 to 5542.
Simples!
I am often met with the question: ‘How do we fit this in with all of the content we need to cover?’
It’s worth pausing to remind ourselves what our objectives as educators actually are:
Mastery of the curriculum requires that all pupils:
- use mathematical concepts, facts and procedures appropriately, flexibly and fluently
- recall key number facts with speed and accuracy and use them to calculate and work out unknown facts
Teaching for Mastery: Questions, tasks and activities to support assessment
NCETM and Oxford University Press (Oxford OWL), 2015
It’s not a case of fitting in opportunities to promote the use of maths facts and flexible thinking; it should permeate everything that we do, within and beyond mathematics.
That’s how we ‘fit it in’.
Click here to attend the next Maths Subject Leader Briefing Autumn 2022 led by Sarah Carpenter and Jason Horne. This is an online Zoom meeting to share tips, best practice and discuss relevant topics.
About the Author
Before moving to Kent, Sarah lived in West Berkshire and led improvement in a range of areas including SEND, Maths and Literacy and Early Years (Communication, Language and Development).

Sarah is passionate that pupils receive the very best teaching possible, and keeps her knowledge of the latest pedagogic research and developments up to date in order that she can pass that knowledge on to assist others. She leads in-school support and training in all elements of literacy and maths.
Sarah specialises in:
English subject knowledge:
- reading and phonics
- writing
- grammar, punctuation and spelling.
Maths subject knowledge:
- using manipulatives from EYFS to Year 6
- developing fluency, reasoning and problem solving
- promoting opportunities to work at greater depth.
Subject Leader support and development:
- joint learning walks and work scrutiny.


