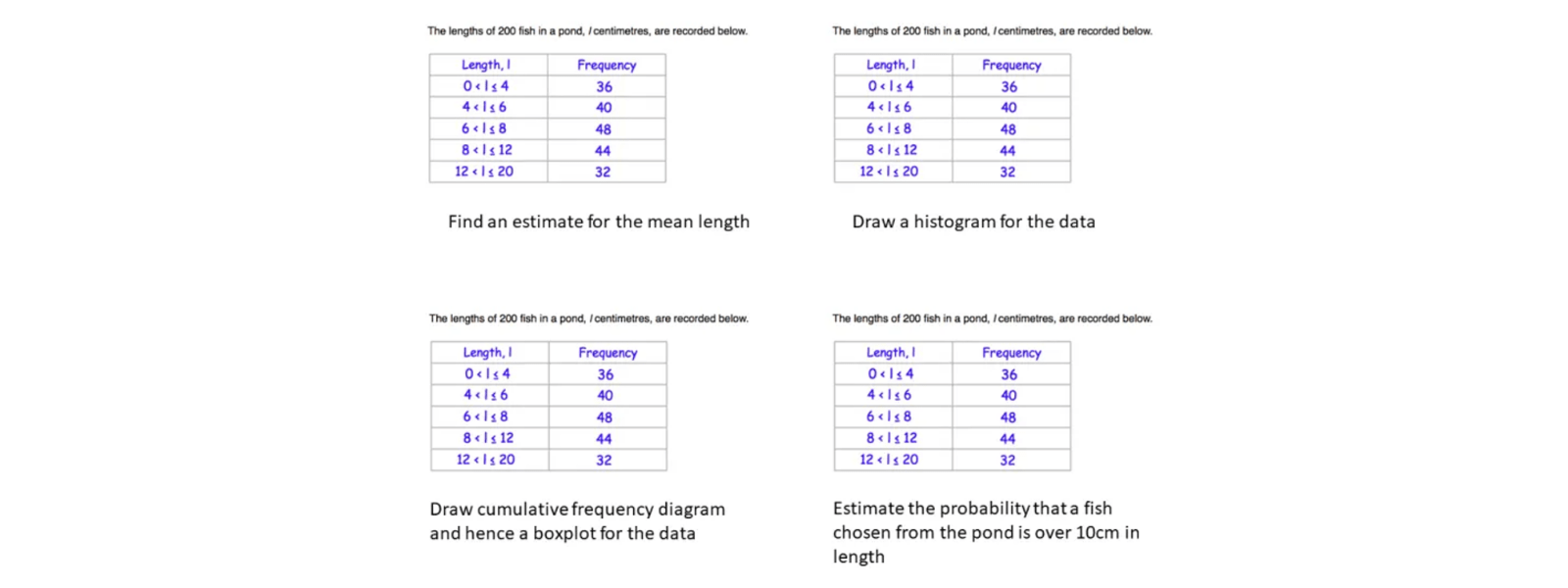
Lesson Planning: Estimating the Mean from Grouped Data

Lesson planning is both an art and a science. Tailoring it to your class and what their strengths and weaknesses are, combined with evidence informed practice, is a challenge. What I hope to do is just share one example of some planning for teaching-how to estimate the mean from grouped data.

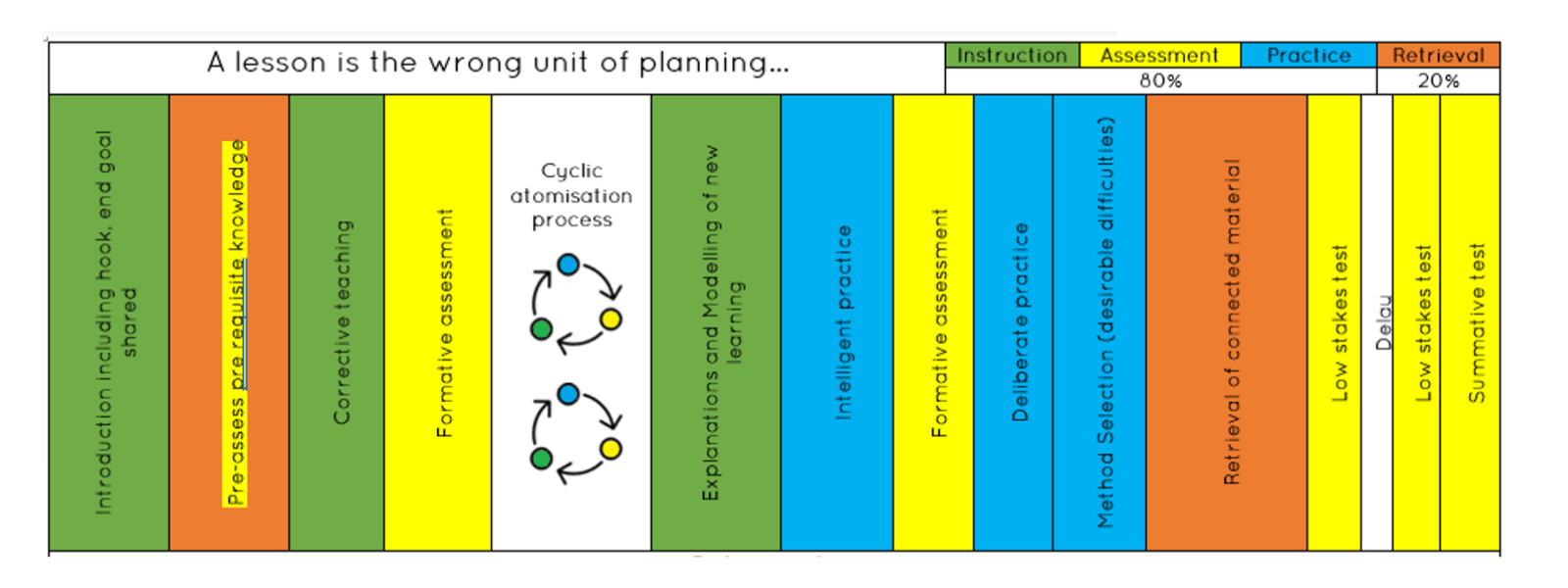
I feel this diagram helps contain some of the helpful prompts of evidence informed practice and bring them all together in a helpful pathway. Although, teaching is certainly more dynamic than this, it is helpful knowing when to bring in various tools and strategies and when to leave them out because they are not needed.

So here is my walkthrough on how I might approach this planning pathway for estimating the mean from grouped data.

Firstly, I would discuss something like this.

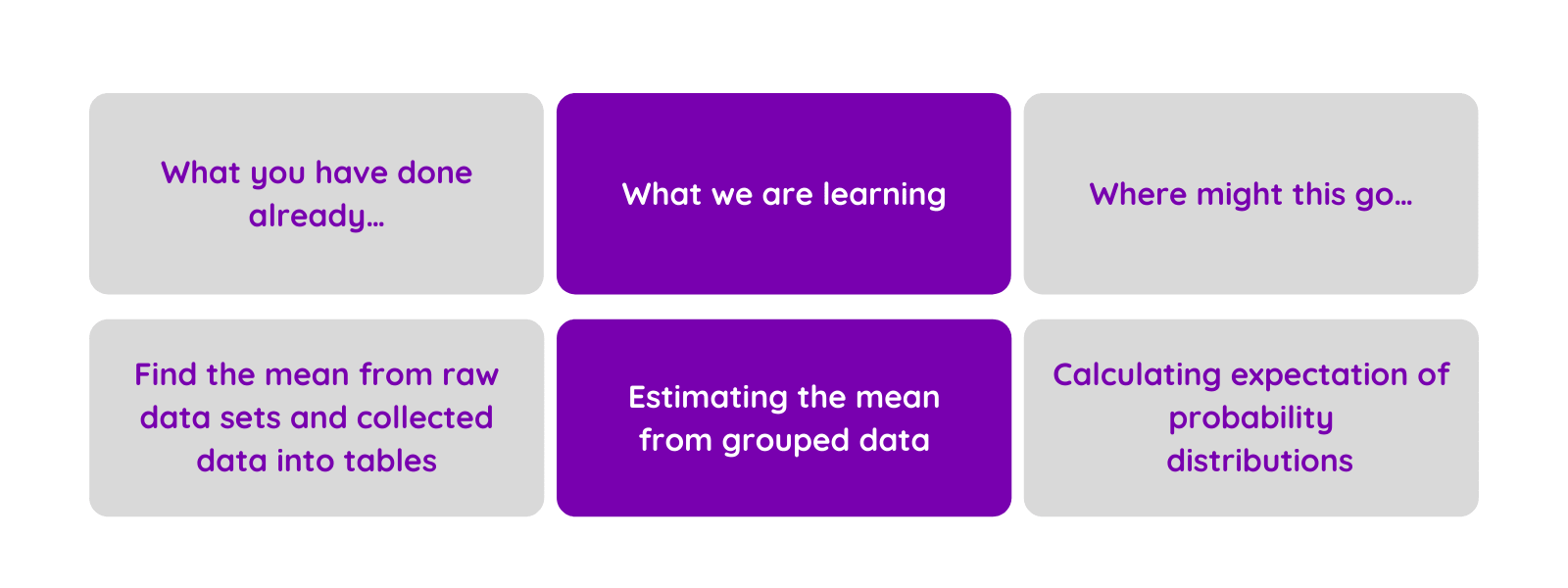
This is tapping into ‘The Elaboration Theory of Instruction’ helping students see how the current learning sits in a bigger picture of mathematical learning. This helps posit the learning and also to prepare them to assimilate into their prior learning and connected topics.

Assessing prior knowledge becomes important to know where to start. This is because what students know will determine what they learn [Expertly summarised in a blog here].

With this topic I would be keen to assess their understanding on what they understand by the mean.  Importantly though, not just can they calculate the mean. Through some quick-fire diagnostic questions, you can quickly gage where a class sits in their current learning.

Supporting these prerequisites, I might return to a few visuals to illustrate the concept if required.

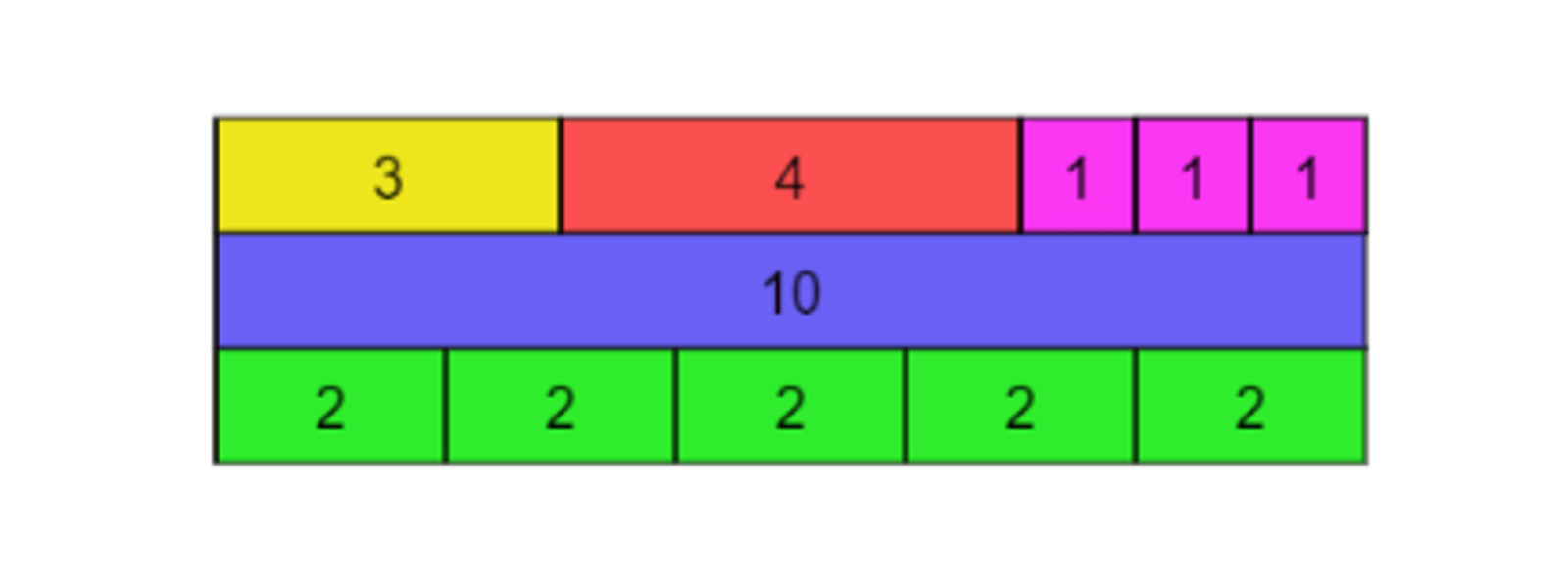
a. Levelling off

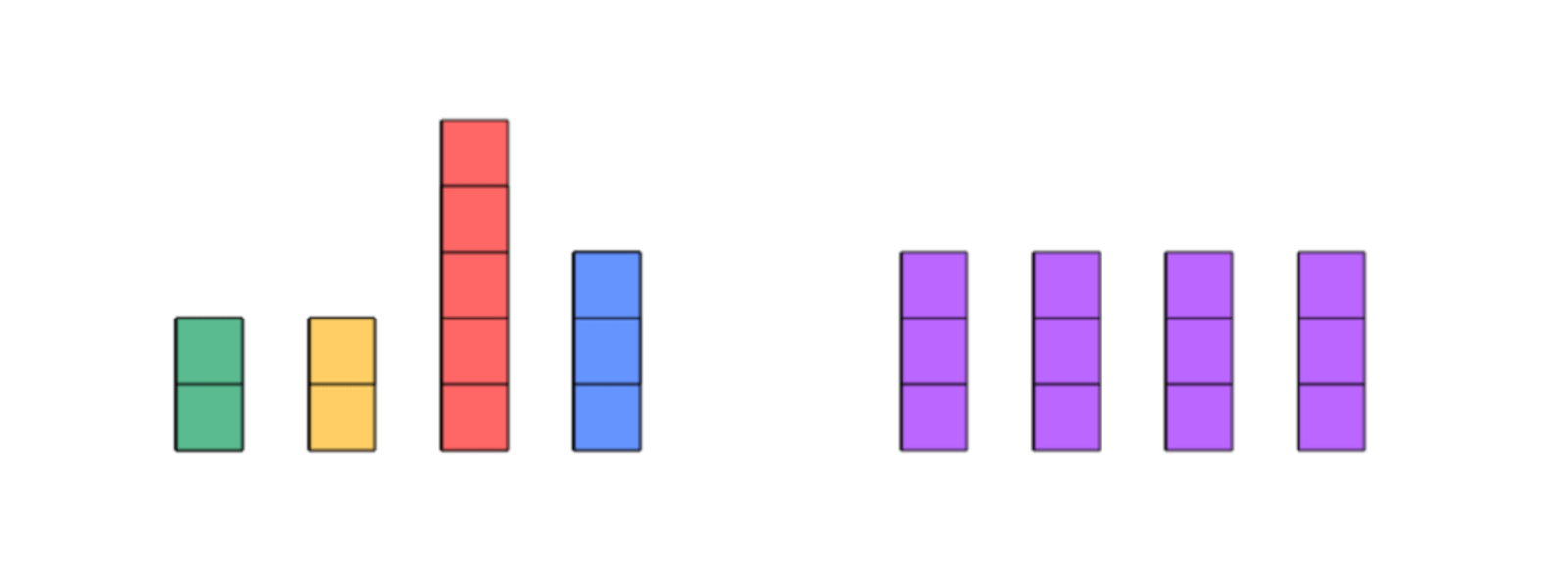
b. Bar modelling sharing out equally

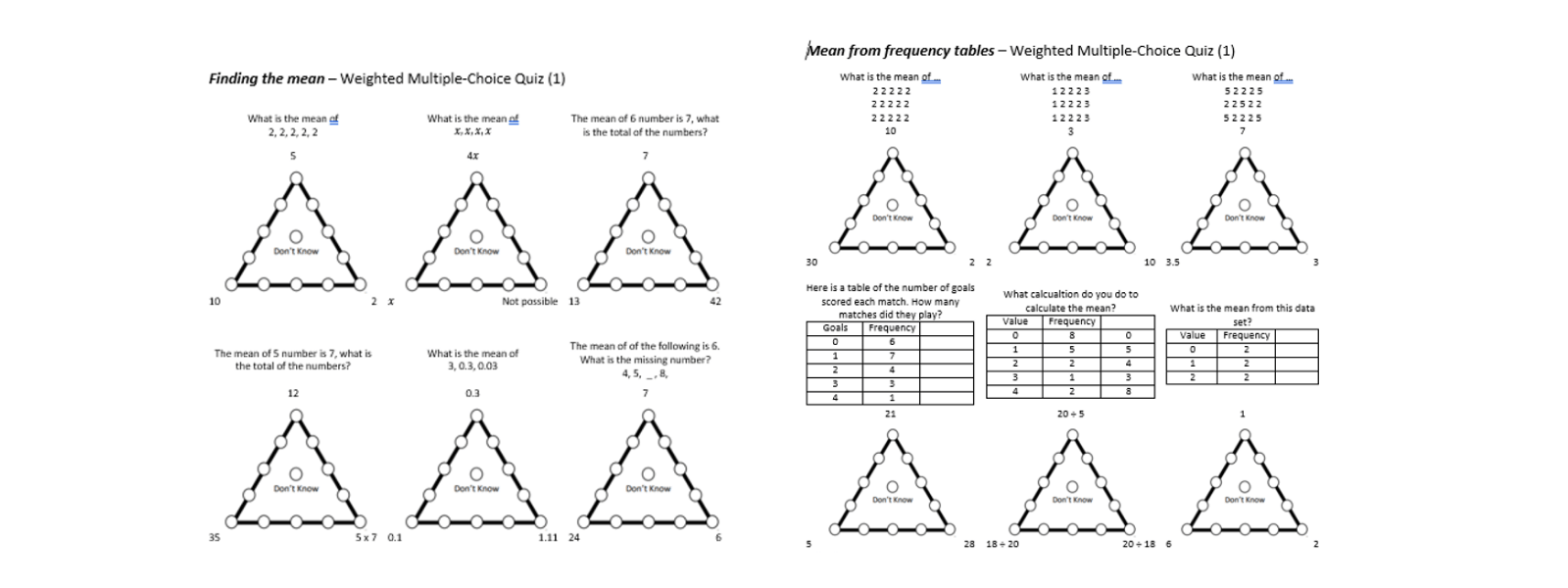
I would then assess how this has gone and want to reinforce previous learning. This can be done pre and post revisiting the prerequisites. I would use these confidence weighted multiple choice quizzes that I have recently blogged about.

New material

Breaking up a complex multi-step process into small steps is important to ensure working memory is not over loaded. Working through cycles of instruct, practice and assess. This is because if students have information embedded into their long term memory and are fluent in the retrieval of this information, this results in less pressure on working memory for the complex task at hand. To do this I would use both example problem pairs and questions from variationtheory.com.

A bridging task can then be used to connect the prior leaning to the new learning. This task by Colin Foster is a great task to help students make those links to how data collection tables are used and the understanding that the multiplication is repeated addition. This task helps us to have a discussion on how to calculate the mean from an array of numbers. This then naturally falls into various methods of speeding the process up by groupings.

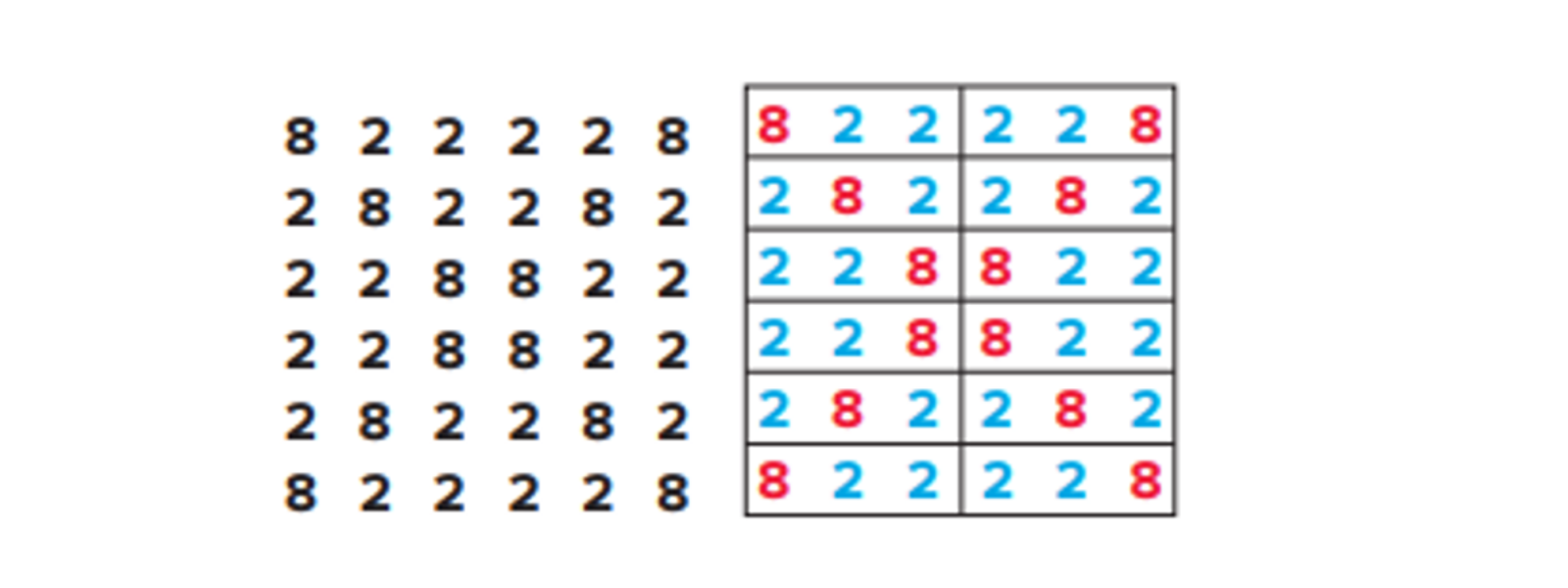
Using prompts like: how would you calculate the mean from this data set? Can you spot any patterns? Can you spot any short cuts?

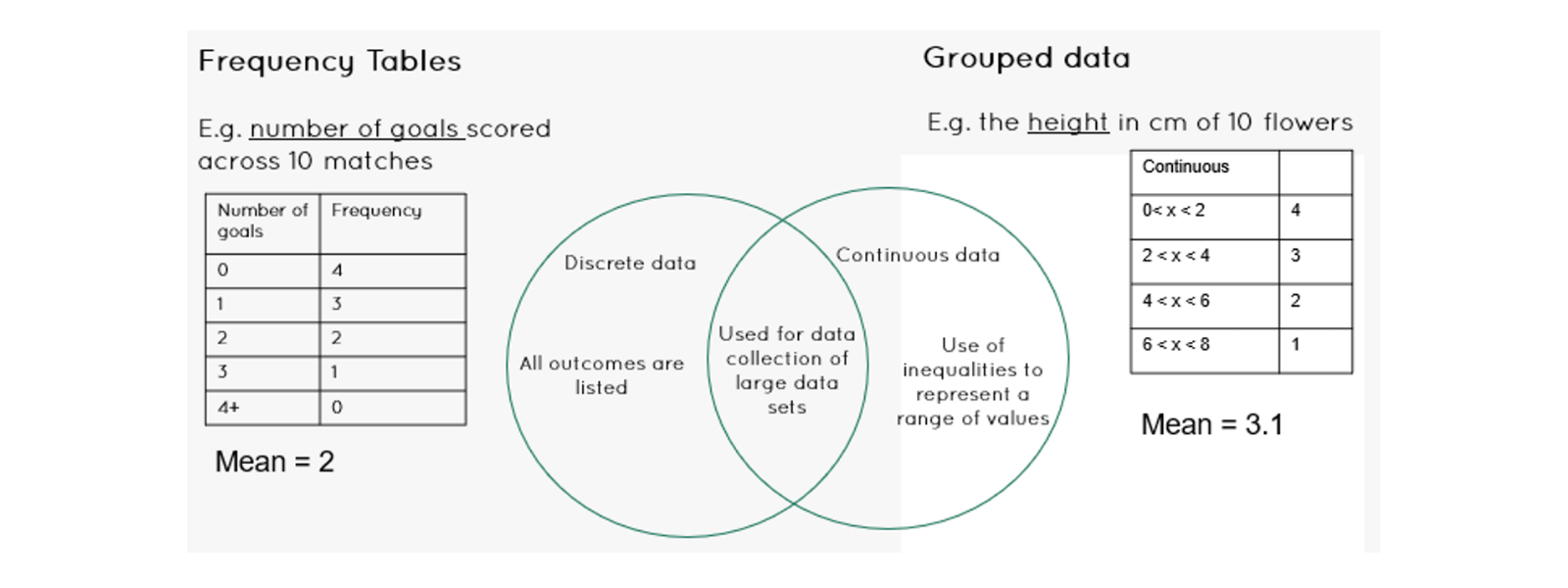
After building confidence in how these arrays form frequency tables it is worth talking about when we might need groups for continuous data. Distinguishing similarities and differences using a Venn diagram can also be helpful as an aid of method selection later. Within this instruction phase highlighting the various pros and cons for grouped data are important. In particular, drawing attention to the fact we lose the exact values of the data in grouped data.

Modelling, narration and lots of questioning of the new skill is required. Using visual representations as required to help students understand the structure. Frequent use of the questions like: why are we using the midpoint? Remind me, do we know the raw data? Can support understanding as they progress.

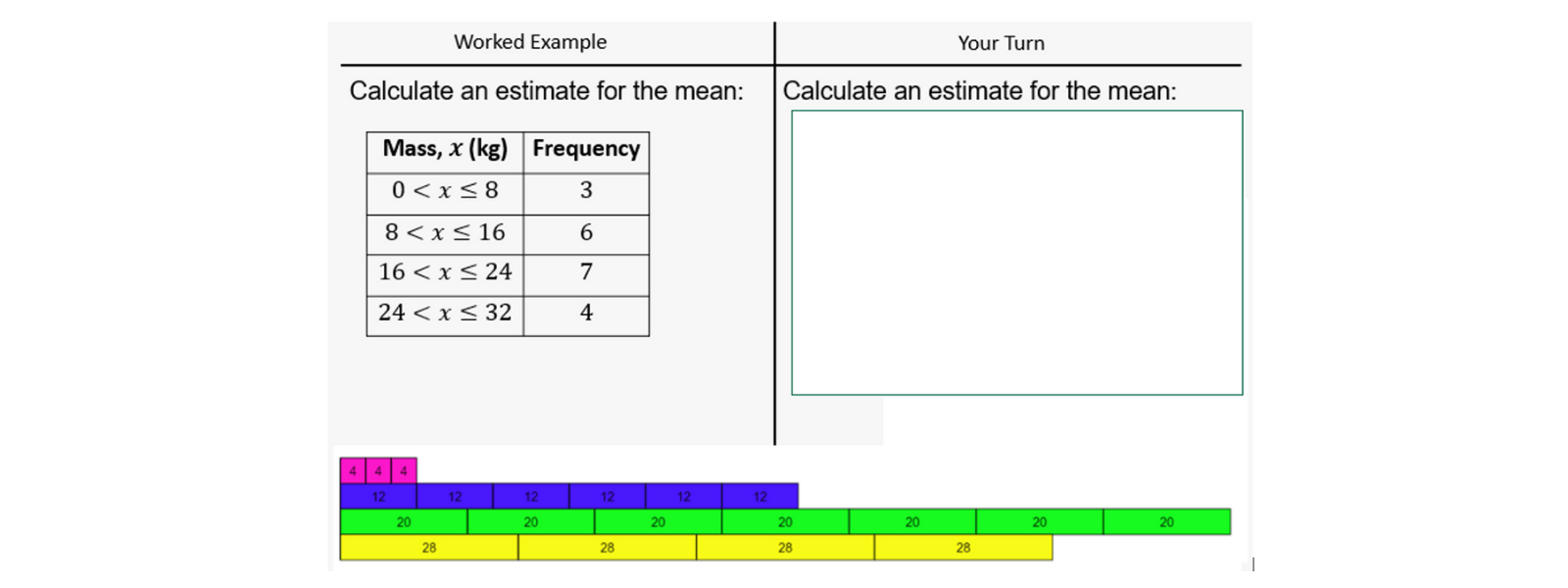
Then providing intelligent practice tasks to help develop deeper understanding through various cause and effect of variation. This is something Mr Barton explores in much more detail within his blogs and resources through the use of prompts such as Reflect, Expect, Check, Explain.

Retrieval of connected ideas

Retrieval of connected ideas means to return to topics that are related to, but not explicitly in, the new material. These are often topics they have studied previously but by returning to them it allows students to mature in their understanding. Maturation in maths is a complex field and one that might require a further blog – but essential the idea is that as students are exposed to more interconnected mathematical content, they naturally form a better understanding of previous learning. In particular, they have developed new ways in which to engage with the maths as a mathematician. Therefore,  returning to these topics in an enriching way can be extremely helpful to strengthen retrieval fluency and build and reorganise their schema.

When searching for tasks that do this, my go to website is of course Don Stewart’s. Often these tasks are so well thought out that students don’t fully appreciate the fullness of these tasks when they might first come across the studied topic. But as students mature, returning to these can provide great richness to their behaviours as a mathematician. For example, this task might be something I do to round off this learning episode on estimating the mean from grouped data. The origins of the task are acknowledged as coming from Mary Rouncefield, Chester University and Peter Holmes.

Q) Estimate the mean diameter of all the circles on the sheet by picking a smallish sample (eg. five circles).

From this task lots of rich discussion can be had which is detailed within the resource on Don Stewart’s blog. In particular, developing behaviours as a mathematician of what is fairness and why it's important. Not to be understated but this task engages students in what estimating the mean is but from a starting point in which they are already confident with.

Assessing learning is important and to ensure that assessment is checking for learning being a change in long term memory. A short delay period and then returning to a low stakes quiz (like the ones I’ve created as confidence weighted questions) can then be used to assess how successful students have been with the material. How long this delay is, is up for debate, but it is agreed that 3-5 days might be a good timeframe for an initial delay.

Finally, planning for future retrieval lessons when teaching connected topics and method selection becomes important. Then tasks such as same surface different depth can be helpful with this, like the one below.