How to Support Problem Solving by Making it Difficult

When does helping become unhelpful? I was considering this with a trainee teacher this week and we started discussing how we do not always want to smooth the path of learning for our students.

Sometimes helping is unhelpful.

Finding that right level of help is important. Help too much and it might develop into an unhealthy reliance creating students who enjoy being spoon feed. Go too far the other way and learners are left to themselves to make sense of the content and this is not going to be very efficient.

As with many aspects of teaching a happy medium might be sought. Important to this idea is that learners are not as fragile as we might think. A term coined by Nassim Taleb, antifragile, can be helpful here. Antifragile is the idea that the experience of difficulties and struggles subsequently strengthens and reinforces what is being stressed.

Let me give a personal physical example that I have been experiencing recently. I have had an ongoing injury in the ball of my right foot preventing me from walking. Pain in my foot was telling me to stop and rest and take the weight off it. Unfortunately, this became an unhealthy cycle in which during the period of non-weight bearing my foot muscles wasted away. Consequently, it was even more painful to weight bare. To end this cycle, I needed to adopt a mindset of antifragility. I needed to work through pain and be confident enough (through reassurance of professional opinion) that my foot is antifragile and will strength through increasing the stress and load. It worked. Attempting to protect my foot due to pain had the reverse effect and actually made it worse.

I think this same idea can be true for learners. If we do not expose learners to struggles and difficulties, then we can inadvertently have the reverse effect. It goes without saying that learning should still take place within a safe, supportive and rigorous environment but leaving space for struggle and difficulty can also enhance learning.

An antifragile mindset can be particularly important when attempting teaching problem solving in maths. Here I am defining problem solving to mean attempting a novel problem in which they have sufficient background knowledge to access the problem i.e. they are not a novice in the content. In order to achieve this, students need to go through and experience difficulty. To do this we should encourage risk taking and not intervene too quickly. Training learners to feel comfortable in the uncomfortable will lead to them developing their problem-solving resolve.

Maths can evoke, for many, a sense of anxiety of not knowing how to tackle a problem. Combatting this classroom climate is crucial. Becoming aware of anxious feelings and acknowledging them can become the beginning of fruitful thought that enables discussion. Focusing on what can be learnt through making mistakes and that mistakes offer powerful learning opportunities can help elevate these feelings. As research from Bjork and Bjork indicates learners need to know this will lead to a decrease in performance and why this is necessary.

“Conditions of learning that make performance improve rapidly often fail to support long-term retention, whereas conditions that create challenges and slow the rate of apparent learning often optimize long-term retention.” (Bjork & Bjork, 2015)

Learning- that is, the permanent change in knowledge or understanding—is something we must try to infer by assessing it after some time has passed. Therefore, we must be aware of not focusing too heavily on poor proxies of performance learning when attempting to train students in problem solving.

Here are a few to be wary of:

• students are busy and lots of work is completed
• students are engaged, interested, motivated
• students are getting attention and feedback
• the classroom is clam and under control
• curriculum has been ‘covered’
• students have supplied correct answers.

Bjork and Bjork’s (2011) work on desirable difficulties nicely encapsulates some proven ways in which altering the right things can enhance learning. These approaches have demonstrated that conditions that slow the rate of learning tend to improve later retention. These are:

1) Varying practice

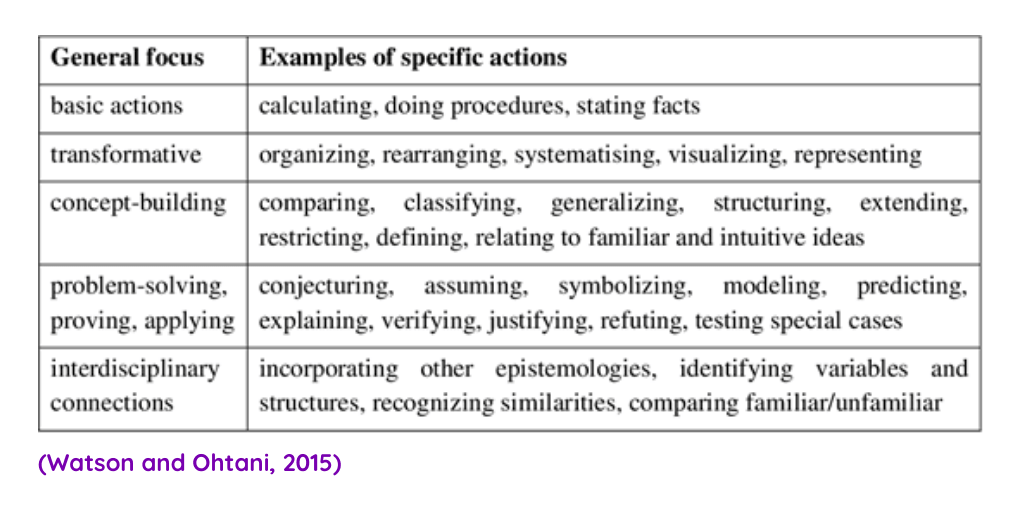
Within maths teaching this, for me, is about approaching lessons in various ways through different pedagogical diets. Worked examples and problem pairs followed by fluency questions are great but if that’s the only diet students receive, they will lack the tools required to work with novel problems. In order to help develop successful problem-solving skills various experiences will need to be considered within the curriculum ensuring students have a balanced diet. A more layered approach is likely to be more successful. A table summarised by Watson and Ohtani in their book describes some of these various focuses and how this will lead to different approaches within the classroom.

2) Spacing study

Little and often is more effective to student learning than massed practice. If a student is to complete 30 questions on a topic, the findings suggest that they would retain the learning better if they did 10 questions each week on this topic spaced over three weeks than all 30 in week one. The implications of this are that curriculum planning is likely to be messy with regular opportunities to return to previous work.

If I look at these findings through the lens of problem solving, then I interpret this also to mean that problem solving (as defined earlier) should be a regular feature in lessons throughout schooling and not massed during exam preparation. Students need regular exposure to the necessary experience of struggle and difficulty.

3) Interleaving vs blocking

Blocking is popular with students as it feels like you are learning in the moment. But the reality is that they have been well primed for answering a question, they have been conditioned in time to answer a similar question. This leads to a false sense of learning. However, interleaving introduces some difficulty where students can be thrown off and directed away from a concept to then return to it. I have seen this been used successfully within tasks to great effect where the current topic questions are disrupted with an alternative topic that students need to stop and think differently to solve and then return to the current topic. This disruption is slowing the learning down but also drawing attention to method selection.

4) Generation effect and using tests

Bjork and Bjork (2011) also conclude that students being able to generate an answer themselves has greater benefits for long term retention than simply being presented with an answer or model. However, this is only suitable for those that have secure domain knowledge that they can reach this point of generation. Asking a student to achieve generation without the required knowledge will prove unhelpful. With problem solving it is not feasible to model every scenario but to develop the student’s own ability of generation should be sought. Bjork and Bjork (2011) also highlight the power of using tests as a learning tool and how this can be beneficial to student learning.

See my previous blog about Weighted Multiple Choice Questions

Not all difficulties are desirable. Making all your students write with the wrong hand is unhelpful. But there are number of difficulties that can enhance student learning: varying practice, spacing study, interleaving, generation and testing. All of which when considering problem solving can slow learning and support the skills required to solve novel problems. This is possible because student learning is antifragile – introducing some difficulty and disruption will strength their long-term learning.