The Concept of Zero: The Greatest Discovery of Nothing

In our most recent Maths Network Meeting, we shared stories that aimed to raise expectations of what students know. With the attempt to start the self-fulfilling cycle of the Pygmalion effect which is proven to improve learners’ performance (Raudenbush, 1984, p.85-97). In particular, we shared stories of mathematicians and events that have made maths the discipline it is today.
For example:
The drowning of Hippasus
Hypatis of Alexandra accused of witchcraft
Guass baffling his primary school teacher
Galois’s gun dual
Why do we use x?
Why is there 360 degrees in a circle?
But the one I wanted to write more about was where zero came from and why it was so important - even to classrooms today.
Humans have always appreciated a concept of nothing. You can almost imagine the early humans grunting for the lack of food or water or that nothing is on TV. Even in Genesis it documents a concept of nothing “And the earth was without form, and void”.
But the modern concept of zero is relatively new in the grand scheme of things. It was only in the fifth century where the introduction of a numeral was used for zero. Previously, the Babylonians (circa 300 B.C.) left an empty space in their number system, but when that became confusing, they added a symbol for zero as placeholder in the form of a wedge. A Persian mathematician, Al-Khwarizmi, made the most of using this placeholder, using it to develop quick methods for multiplying and dividing numbers, which were later known as algorithms — unfortunately recent events have meant he has gained a bit of a bad reputation.
But it still did not have the concept of zero we now know. The zero we have come to know has its roots first in India in 458 AD (Ghevergese, 2010). The Indians Zero (shunya, in Sanskrit) meant ‘void’ or ‘empty’. It was the Indian mathematician Brahmagupta (650 AD) who then penned standard rules for reaching zero through addition and subtraction as well as the results of operations with zero. These have since been refined and are contain with the 9 field axioms of mathematics. Introducing learners to this idea of zero, through the use of double-sided counters in a series of pattern spotting activities, can be extremely helpful.
Eg the existence of the additive inverse creating a zero pair
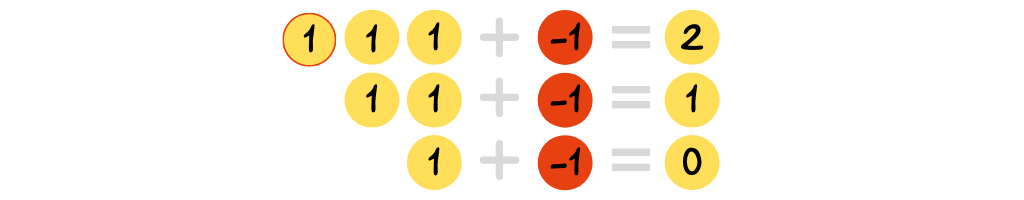
And the additive identity (also shown as a zero pair)
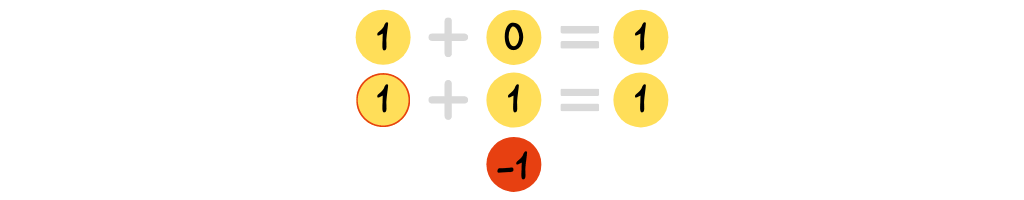
The use of zero pairs can then help students understand what it is they do when subtracting a negative number.
Eg if we wanted to do 4 – (-1). We know that:
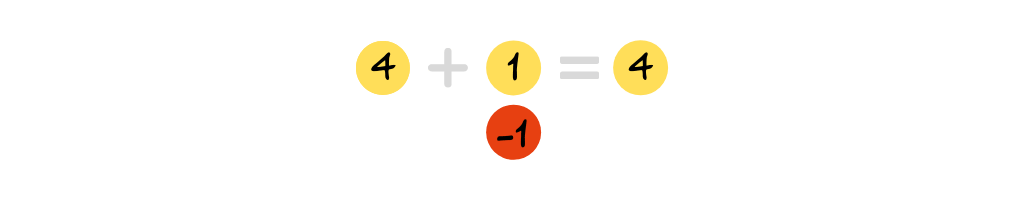
So, if we subtract/takeaway the (-1) we are left with…

The only omission in Brahmagupta’s rules was division by zero, which had to wait for Isaac Newton and G.W. Leibniz to tackle in the late 16th Century. Division by zero has confused even the greatest of minds because the metaphors used in teaching seem to break down…
E.g. How many times does zero go into ten? Or, how many non-existent counters go into four counters?
But Newton and Leibniz laid the foundations for Cauchy (1821) to look instead at taking limits and looking at the behaviour of functions as they approach zero. In the case of differentiation by first principles this allows a concept of dividing by zero to be considered. Thus, enabling us to calculate the gradient functions which then helps interpret multiple fields of maths; including kinematics where we can connect displacement, velocity and acceleration.
Exposing students to alternative base systems other than base 10 can again provide historical context to explain imperial units and why there are 360 degrees in a circle. Since one of the most prolific applications of zero is in the world of computing and the binary base system. This created a divided world splitting the population into 10 types of people. Those who know binary and those who don’t. Teaching beyond the curriculum can ensure students fall into the former.
Zero is a concept that has a rich past and one that is not fully explored here. Sending learners off to do their own research can be one way in which learners develop a better understanding of maths as a discipline. But certainly, bringing in historically stories to the classroom peaks learners’ interest and cultivates an appreciation for the subject beyond the scope of a specification. Time spent researching a story or two can create those moments where learners are hooked and walk out of your lessons wanting to share what they have learnt with others.


